Une calculatrice "en ligne"
Présentation
Images
Description
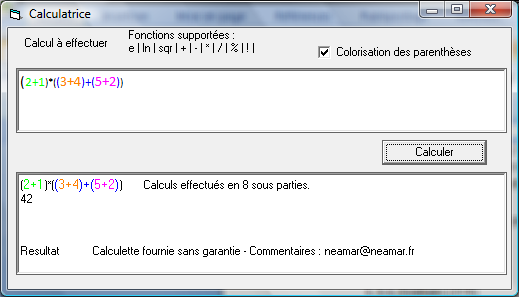
Vous en avez marre de ces sources de calculette qui se contentent de vous offrir des boutons ?(sqr(e(ln((1+3)*(1/(2^2))))))^2
Il faut bien penser que les maths ne nous simplifient pas le travail : priorité des opérations, parenthèses (le code 2(2+1) = 2*(2+1) n'est pas forcément évident !)...
Cette calculette semble bien s'en tirer...cependant, j'ai commencé à la programmer il y a 48h, il est donc possible que certains bugs se soient dissimulés.
Le code est extrêmement commenté...il n'utilise aucune API, aucune fonction avancée..le calcul est entièrement géré par le module appelé "Théorie". (211 lignes de code // 84 lignes de commentaires)from scratches permettrait ainsi d'exporter le code en n'importe quel langage en moins d'une demie heure, voire même de l'implanter sur un microprocesseur et de lancer sa propre calculette !
Le module "Graphique", quant à lui, "colorie" le code : il met en exposant les puissances, met le contenu des parenthèses en couleur...(utilisation du contrôle RichTextBox 6.0)(41 lignes de code // 8 lignes de commentaires)
Et la Form ne contient que 30 lignes...
La calculette gère les opérations standards : + - * / % (modulo), et ! (factorielle),ainsi que e (exponentielle), ln (logarithme népérien),tan et atn, avec gestion des priorités! C'est à dire que : 1 + 2/2 = 2
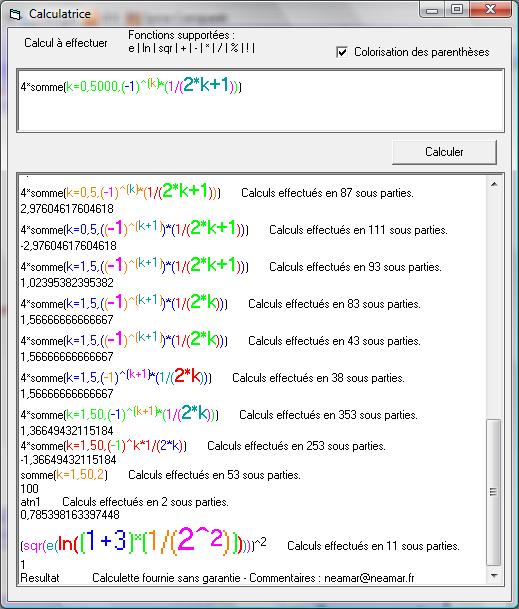
Il y a aussi un outil somme, qui s'utilise de la façon suivante :somme([Nom_Variable]=[départ],[Arrivee],[Calcul])
Cette somme est incorporable dans n'importe quel calcul, et vous pouvez même effectuer des sommes à l'intérieur de sommes à l'intérieur de sommes à l'intérieur de sommes...bref!4*somme(k=0,5000,(-1)^k *(1/(2*k+1))) .
Plus d'informations
Si vous ne comprenez pas tout, lancez un calcul, et regardez la fenêtre exécution : elle affiche en temps réel les calculs effectués.
Par exemple :
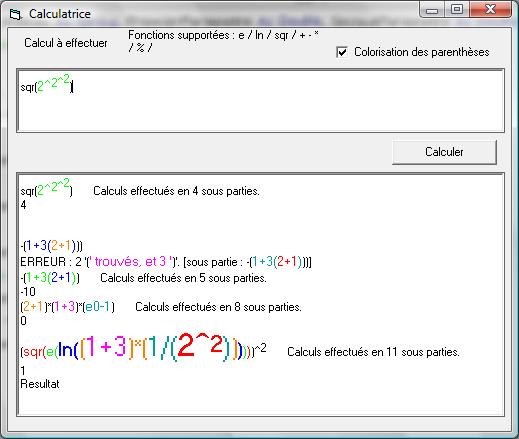
Initialisation du calcul (sqr(e(ln((1+3)*(1/(2^2))))))^2
-------------------------------------------------------
Math_It va effectuer le calcul (sqr(e(ln((1+3)*(1/(2^2))))))^2
Math_It va effectuer le calcul sqr(e(ln((1+3)*(1/(2^2)))))
Math_It va effectuer le calcul (e(ln((1+3)*(1/(2^2)))))
Math_It va effectuer le calcul (ln((1+3)*(1/(2^2))))
Math_It va effectuer le calcul ((1+3)*(1/(2^2)))
Math_It va effectuer le calcul 1+3
Math_It va effectuer le calcul 3
3 a renvoyé 3
1+3 a renvoyé 4
Math_It va effectuer le calcul 1/(2^2)
Math_It va effectuer le calcul 2^2
Math_It va effectuer le calcul 2
2 a renvoyé 2
2^2 a renvoyé 4
1/(2^2) a renvoyé 0,25
(1+3)*(1/(2^2)) a renvoyé 1
ln((1+3)*(1/(2^2))) a renvoyé 0
e(ln((1+3)*(1/(2^2)))) a renvoyé 1
sqr(e(ln((1+3)*(1/(2^2))))) a renvoyé 1
Math_It va effectuer le calcul 2
2 a renvoyé 2
(sqr(e(ln((1+3)*(1/(2^2))))))^2 a renvoyé 1
Comme vous le voyez, le calcul se décompose sous plusieurs formes très simples...(ce qui est, rappelons le, le but de la récursivité !)
De plus, le code est extrêmement souple : si quelqu'un voulait par exemple créer un grapheur, il n'y aurait pas de grosses difficultés.
A propos du débordement
Téléchargement
Ce fichier n'est disponible que pour Windows, car il a été écrit en Visual Basic.
Fichier ZIP (EXE + Sources)
Fichier EXE
Code source
Feuille
Code source : Calculette.frm
Langage : vb Taille : 2569 caract�res '2008 Modules
Module Théorie
Code source : Theorie.bas
Langage : vb Taille : 17137 caract�res Option Explicit Module Graphique
Code source : Graphique.bas
Langage : vb Taille : 2113 caract�res Option Explicit