Dix énigmes ont été sélectionnées pour ce texte.
Elles sont toutes exceptionnelles, que ce soit par leur énoncé, leur solution ou les méthodes à mettre en œuvre pour les résoudre.
Elles requièrent très peu de connaissances mathématiques, mais elles risquent de mettre votre logique à rude épreuve.
L'ensemble est intercalé de façon plaisante dans une aventure au pays mathématique, dont le protagoniste ne sortira pas indemne...
Les 10 plus belles énigmes
Neamar
Un problème de balance
Il n'y a bien qu'à moi que ça arrive, des galères comme ça.
Il n'y a pas dix minutes, j'étais tranquille dans ma chambre, à faire mes exos de maths, et maintenant…
Alors que je venais d'avoir l'intuition qui me permettrait de résoudre mon problème, je me suis retrouvé dans cette pièce aux murs blancs. Et quand je dis retrouvé, c'était direct : on aurait presque dit de la téléportation. Mis à part que la téléportation, ça n'existe pas…
Devant moi se tenait un colosse, en costume cravate, qui ne parut même pas surpris par ma brusque apparition.
Il me dévisagea rapidement, avant de me tendre sans un mot un petit sac fermé par une lanière de cuir. Intrigué, je défis la lanière pour jeter un rapide coup d'œil à l'intérieur : il n'y avait que des billes, le même genre que celles avec lesquelles on joue quand on est gamin. Je levai les yeux, interrogateur, lorsqu'il prit enfin la parole :
« Ce sac contient 80 billes. Elles sont toutes exactement semblables, sauf l'une d'elles qui est légèrement moins lourde… mais qui a la même apparence extérieure que les 79 autres. » Il fit un pas de côté, me dévoilant une balance que sa stature avait maintenue cachée jusqu'ici. C'était l'un des ces antiques modèles à plateaux, qui permettait uniquement de comparer deux poids entre eux.
L'homme reprit :
« Tu as 4 pesées à faire. Au terme de ces 4 pesées, tu devras me donner la bille différente. »
Avant de me laisser le temps de lui poser une question, il se posta derrière moi… et devant la seule porte. Je ne sais pas pourquoi, mais je n'avais pas l'impression qu'il était là pour rigoler. Et de toute façon, j'avais toujours été attiré par les énigmes. Alors, autant tenter ma chance, non ?
Solution no1
La première idée qui me vint à l'esprit fut de faire deux paquets de 40 billes, et de les peser. Je prendrais alors les 40 billes sur le plateau supérieur (ce paquet étant plus léger que l'autre, la bille moins lourde s'y trouve forcément), recouperait en deux tas égaux de 20 billes et reproduirait le même raisonnement (j'aurais donc à l'issue de cette seconde pesée 19 billes normales plus la bille légère), avant de recommencer à nouveau (avec 10 billes de chaque coté), et encore une fois (5 billes). Le problème, c'est qu'au terme de cette quatrième et ultime pesée, il me resterait encore 5 billes ; et plus aucun moyen de les différencier.
Cependant, cette méthode de « couper en deux » à chaque passage me rappelait vaguement une notion de mon cours de maths – la dichotomie – qui fonctionne exactement sur le même principe (dichotomie vient du grec et signifie « couper en deux »). Dichotomie… Di-chotomie ! Et pourquoi ne pas essayer avec la tri-chotomie ? Car en y réfléchissant bien, ma première méthode n'exploite que deux possibilités de la balance : à gauche et à droite. Mais la balance peut aussi donner une autre information : égalité !
Je fis mentalement le schéma de la marche à suivre : séparer en trois tas les plus égaux possibles (soit deux tas de 27 et un tas de 26 car $\frac{80}{3}=26.\bar{6}$), et peser les deux tas de 27 (appelons les A et B, et C le paquet de 26 billes).
- Soit la balance penche du coté de A, et je sais alors que la bille cherchée est dans B ;
- Soit la balance penche du coté de B, et je sais alors que la bille cherchée est dans A ;
- Soit A et B sont de même poids, et je sais alors que la bille cherchée est dans C.
J'obtiendrais alors un tas de 27 billes au maximum contenant la bille spéciale. Je re-divise ce tas en trois (soit trois tas de 9, ou deux tas de 9 et un tas de 8 si la bille est dans C).
En rappliquant le même protocole, j'obtiens un tas de 9 billes maximum contenant l'intruse, et cela en seulement deux pesées ! Il ne me reste plus qu'à recouper en trois mon échantillon (soit des paquets de 3, ou deux paquets de 3 et un paquet de 2), peser, récupérer le bon tas, et avec ma quatrième pesée mettre une bille de chaque coté : soit ça penche d'un coté et la bille cherchée est alors de l'autre côté, soit ça ne penche pas et la bille est alors celle qui me reste dans la main : dans tous les cas, je suis sûr d'avoir juste !
Un petit sourire aux lèvres, et plutôt fier de moi, j'appliquai donc mon algorithme fraîchement trouvé ; et je me retrouvais, comme prévu, avec une seule bille, la plus légère. Confiant, je me retournais pour la donner au colosse… avant de m'apercevoir que celui-ci avait disparu, laissant derrière lui la porte ouverte. Poussé par la curiosité, et n'ayant de toutes manières aucune autre alternative, je sortis donc de ma pièce pour arriver face à une immense avenue bordée de maisons aux formes bizarres : les numéros aux portes étaient des lettres grecques, et l'on pouvait apercevoir que les rares arbustes qui poussaient dans les jardinets avaient des racines carrées.
Mais dans quoi me suis-je encore fourré ?
Pour en savoir plus : La dichotomie
Un étrange testament
Dans l'avenue, trois jeunes se disputaient. Dès qu'ils me virent, ils me fondirent dessus pour m'expliquer leur contentieux. Les trois parlaient vite et en même temps, et je dus les forcer à stopper pour pouvoir y comprendre quelque chose. Celui qui semblait le plus âgé reprit, seul, la parole, et à un débit plus raisonnable :
« Nous sommes trois frères, et nous venons de perdre notre père. »
Au ton dégagé qu'il prit, je compris qu'exprimer mes condoléances serait non seulement superflu, mais aussi complètement hors de propos.
« Il avait une richesse colossale : 17 lingots d'or sculptés et aksodazés.
Avant de diverger vers l'infini, il nous a laissé son testament – un testament assez spécial ».
Je ne pris pas la peine de demander ce que signifiait “aksodazer”, et me concentrait de nouveau sur son récit :
« À son premier fils, c'est à dire moi, il lèguerait la moitié de ses lingots. C'est normal, car j'étais son préféré (les deux autres firent la moue, mais ne dirent mot).
Au second fils, il donnerait le tiers de sa fortune.
Et au troisième, le neuvième.
D'où notre problème ! Comme tu le sais, l'or aksodazé ne peut pas être coupé, et aucun de nous n'est disposé à abandonner sa part aux autres. Mais 17 n'est divisible ni par 2, ni par 3, ni par 9 ! »
Je compris qu'ils attendaient une réponse de ma part, mais à l'instant même, je n'avais aucune idée… cependant, la perspective de rester au milieu d'eux en leur disant que leur problème m'indifférait n'était guère plus reluisante !
Comment régler leur problème pour qu'aucun d'eux ne se sente lésé ?
Solution no2
Une question restée sans réponse me chiffonnait cependant : le père n'avait cité que ses trois fils dans son testament, et pourtant il n'avait pas légué l'ensemble de sa fortune. Cela se vérifiait facilement, puisque $\frac12 + \frac13 + \frac19 = \frac{17}{18}$.
Tiens, tiens… voilà qui était intéressant ! Puisqu'à priori l'or aksodazé était insécable, le seul moyen de résoudre ce dilemme était d'avoir un nombre de lingots $n$ tel que ce nombre de lingots multiplié par $\frac{17}{18}$ soit un nombre entier. (autrement dit, il fallait que $n \times \frac{17}{18}=\lambda, \lambda \in \mathbb{N}$). Je remarquais directement que $n=18$ correspondait ($n$ se simplifie alors avec le dénominateur…).
Imaginons donc que leur paternel possédait une fortune de 18 lingots.
- Le premier fils récupérerait 9 lingots car $18 \times \frac12 = 9$ ;
- Le second fils récupérerait 6 lingots car $18 \times \frac13 = 6$ ;
- Le premier fils récupérerait 2 lingots car $18 \times \frac19 = 2$.
Et que vis-je alors ? $9 + 6 + 2 = 17$. Autrement dit, s'il y avait 18 lingots, non seulement le testament devenait applicable, mais en plus à la fin je récupérais le lingot virtuel “injecté” précédemment. Ce qui était normal, puisque le testament ne léguait pas l'ensemble de la fortune. Il me suffisait donc de leur faire imaginer un lingot en plus, d'appliquer le partage, puis de récupérer le lingot imaginaire.
Mais respectais-je vraiment les dernières volontés du décédé ? Si je reprenais la fortune réelle, j'avais bien $9 > 17 \times \frac12$, $6 > 17 \times \frac13$ et $2 > 17 \times \frac19$. Autrement dit, chacun des frères toucherait légèrement plus que ce qui était prévu ! Ils n'allaient sûrement pas s'en plaindre – en revanche, le notaire risquait de faire quelques difficultés !
Je leur proposais donc ma solution, qui les enthousiasma rapidement… à tel point qu'ils voulurent partir pour aller rejoindre leur notaire, afin de “récupérer ce qui leur appartenait de droit”. Avant qu'ils ne disparaissent eux aussi, je me décidai à leur poser quelques questions, afin de comprendre un peu mieux cet étrange lieu… et pour découvrir comment rentrer chez moi.
Une question vieille comme le monde…
Je les retins d'un mot avant qu'ils ne partent :
« Attendez ! Avant de partir, j'estime avoir droit à des remerciements… »
Ils se regardèrent, gênés, avant de marmonner un “merci” peu convaincant.
« Ne vous inquiétez pas, je ne suis pas du genre à prendre la mouche pour si peu… je voudrais juste vous poser quelques questions ! Pour commencer, où sommes nous ? »
Comme par magie, cette phrase dissipa le mal être qui s'était instauré, et les trois frères éclatèrent de rire. L'un d'eux répondit à mon regard interrogateur :
« À chaque fois qu'il y en a un qui s'intègre ici, il pose la même question stupide ! Nous sommes dans le noyau central d'un sous espace vectoriel. Chacun des habitants est un rescapé d'une ancienne base… mais ils ont été forcés de quitter notre matrice initiale. Le vieux Supérieur t'en dira sûrement plus là dessus… parce que moi et mes frères, nous sommes des cas un peu particuliers ! »
Oulà. Voilà que je n'y comprenais plus rien ! La seule chose compréhensible semblait, heureusement, être la seule information vraiment intéressante.
« Le vieux Supérieur ? Et il pourrait me dire comment revenir chez moi ? »
Les trois jeunes esquissèrent un nouveau sourire :
« Comme d'habitude… à peine intégré, il veut déjà dériver ! Encore une fois, seul le vieux sage pourra t'en dire plus. Mais je crois savoir que tout cela à un lien avec la maison des constantes… »
J'avais complètement décroché, cette fois ! Après leur avoir demandé où je pourrais trouver ce vieux sage, je les remerciais poliment en insistant sur le mot “merci”, avant de partir vers la maison du Supérieur.
Arrivé à l'avenue où se situait sa maison, j'estimais la distance à 2 kilomètres. Un homme marchait dans la rue, et semblait se diriger lui aussi vers le logis du Supérieur… mais sa démarche était bizarre. Peut être avait-il des problèmes de motricité ?
Je fis un pas en avant… et me retrouvais à un kilomètre de la maison ! J'avais parcouru la moitié de la distance en un pas ; la gravité devait sacrément baisser dans cette avenue !
Je fis un nouveau pas pour me retrouver à 500 mètres de ma destination. J'avais à nouveau fait la moitié de mon chemin – soit le quart de mon trajet initial. Craignant le pire, je fis un nouveau pas et cela n'y manqua pas : je me retrouvais 250 mètres plus loin – le huitième de ma distance initiale. Je compris que j'étais tombé dans un piège lorsque mon quatrième pas m'amena à 125 mètres de la maison… je n'étais pas arrivé ! À chaque pas, ma distance diminuait de moitié… le problème, c'est que de cette façon, je m'approcherais infiniment de la maison, mais ne serait jamais dedans. À moins que…
Solution no3
Je me souviens que mon prof de maths nous avait parlé de ce paradoxe. C'était Zénon d'Élée, un Grec, qui l'avait inventé, quelques siècles avant la naissance de Jésus Christ. Zénon s'illustrera plusieurs fois pour ses paradoxes qui tiendront en haleine la communauté scientifique pendant des siècles. Pourtant, la solution à ce problème était si simple… il suffisait de faire la somme infinie, chose à laquelle les Grecs refusaient de penser. Il est vrai qu'au premier abord, additionner à l'infini des termes semble très abstrait. Et pourtant !
À chaque passage, j'avance de la moitié du chemin restant. Le problème consiste donc à trouver la somme infinie de :
$\frac11 + \frac12 + \frac14 + \frac18 + \frac{1}{16} + \frac{1}{32} + \ldots$
(On utilise les kilomètres comme unité).
Les mathématiques modernes ont développées tout un ensemble d'outils pour traiter ce genre de problème : les séries.
Plus formellement, les scientifiques utilisent la notation $\sum$ (prononcer sigma, ou somme), qui s'utilise de cette façon :
$\sum_{n=0}^{+\infty} \frac{1}{2^n} = \frac11 + \frac12 + \frac14 + \frac18 + \frac{1}{16} + \frac{1}{32} + \ldots$
Cela permet d'éviter les points de suspension qui ne sont pas très rigoureux d'un point de vue formel. Mais peu importe !
Nul besoin de connaissances mathématiques poussées pour résoudre ce problème. Il suffit de le poser bien à plat :
Soit $S = 1 + \frac12 + \frac14 + \frac18 + \frac{1}{16} + \frac{1}{32} + \cdots$
On peut factoriser par $\frac{1}{2}$ : on obtient alors $S = 1 + \frac12 \left( 1 + \frac12 + \frac14 + \frac18 + \frac{1}{16} + \frac{1}{32} + \ldots \right)$, et que voit-on apparaître en facteur ? La somme S !
On a donc $S = 1 + \frac12 \times S \Leftrightarrow S - \frac12 S = 1 \Leftrightarrow \frac{S}{2} = 1 \Leftrightarrow S = 2$. Et voilà ! Et l'incroyable, c'est que ceci est une égalité exacte, pas une approximation…
Autrement dit, en continuant d'avancer jusqu'à l'infini, je finirai par arriver… mais je n'avais pas vraiment de temps à perdre ! D'autant que la personne devant moi continuait de marcher, et semblait faire du surplace… preuve que ce choix n'était pas le bon. Je choisis donc de faire demi-tour… et tentais d'accéder à la maison par le jardin arrière. Miraculeusement, je n'eus plus de problème de distorsion temporelle. Une fois dans le jardin, je réussis à ne pas trébucher sur une des racines carrées qui jonchaient le sol, et me présentait à la porte, le cœur battant et la tête pleine de questions…
Pour en savoir plus : Les paradoxes de Zénon
Pour aller plus loin
Comme je le disais plus haut, les mathématiques ont développées des outils puissants pour analyser ces suites : les séries numériques.
Ainsi, on peut montrer très rapidement que cette série converge, en utilisant les théorèmes des séries à termes positifs. On peut montrer par exemple que $n \geq 5 \Leftrightarrow 2^n \geq n^2 \Leftrightarrow \frac{1}{2^n} \leq \frac{1}{n^2}$. Par comparaison à une série de Riemann d'exposant 2, on a donc prouvé la convergence.
Il reste à trouver vers quoi cela converge : $S = \sum_{n=0}^{+\infty} \frac{1}{2^n} = \sum_{n=0}^{+\infty} \left( \frac{1}{2} \right)^n$ : c'est la somme infinie d'une suite géométrique de raison $\frac12$ : on sait très facilement la calculer (depuis le lycée !) : $\sum_{n=0}^{+\infty} \left( \frac{1}{2} \right)^n = \lim_{n\rightarrow\infty} \frac{1-\left( \frac12 \right)^n}{1 - \frac12} = \frac{1}{1-\frac12} = 2$.
Sans surprise, on retrouve bien le résultat cherché…
Trait Trait Point
Cela faisait maintenant 10 minutes que j'attendais sur le palier de la porte arrière. Mes appels répétés et mes sonneries n'avaient amenés aucune réponse de l'occupant. Qu'étais-je censé faire ? Repartir ? Rentrer à l'intérieur de la maison sans attendre de réponses ? Je soupesais chacune de ces options dans ma tête, et me décidai finalement à entrer : après tout, je n'avais nulle part où aller, excepté cette maison. Et j'avais besoin de réponses à mes questions. Je pris donc la poignée de porte et poussai… sans résultat : la porte semblait verrouillée. C'était bien ma veine ! Par acquit de conscience, je jetais quand même un coup d'œil au verrou. Il était d'une forme spéciale, qui ne me rappelait rien de connu : ce verrou était simplement constitué d'un tableau de trois points par trois points, comme ceci :
$\begin{bmatrix}. & . & . \\ . & . & . \\ . & . & .\end{bmatrix}$
À côté de ce verrou pendait, accroché par une ficelle, un stylo. Juste au dessus du verrou, gravé en lettres majuscules, se trouvait l'inscription très sibylline : « 4 droites sans lever le stylo, 9 points ».
Hum. Je suppose donc que je dois, à l'aide du stylo, tracer 4 droites, et recouvrir les 9 points… voyons ça ! Sûrement rien de bien compliqué.
Solution no4
Après quelques tentatives infructueuses, je dus me rendre à l'évidence : le problème était plus complexe qu'il n'y paraissait. Mon premier trait passait toujours par dessus 3 points, mais aucun des autres ne couvrait trois points. Et mon dernier trait ne surlignait qu'un seul point ! Autant dire qu'un point continuait de me narguer indéfiniment… je pouvais changer de méthode, mais dans ce cas là, un autre point prenait la relève et refusait obstinément de se faire écrire dessus. C'était à se frapper la tête contre les murs… ou contre la porte, solution plus proche et sûrement moins douloureuse.
 Si seulement on m'avait donné un stylo plus épais ! J'aurais pu tricher un peu…
Si seulement on m'avait donné un stylo plus épais ! J'aurais pu tricher un peu…
Et si les points avaient été plus larges, le problème devenait facile : il me suffisait de zigzaguer un peu en dehors…
Au moment même ou cette idée – au dehors – me vint à l'esprit, la solution s'imposa à moi : c'était pourtant évident ! Comment avais-je pu ne pas le voir jusqu'ici ? Il suffisait de penser autrement… j'écrivis immédiatement la solution, comme si je craignais de l'oublier. Mais c'était fort peu probable : je venais de comprendre quelque chose d'important.
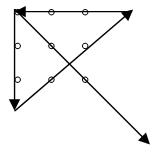
Inconsciemment, je m'étais contraint à rester à l'intérieur du tableau défini par les trois points. Mais c'était une mauvaise utilisation de l'espace qui m'était alloué : après tout, aucune règle ne me donnait une limite de taille ! Je m'étais auto-bridé, j'avais laissé mon subconscient décider à ma place ! Et je venais de comprendre mon erreur : chaque vérité n'est vraie que dans un cadre donné. Il suffit de changer un minimum les règles pour que ce qui était vrai devienne faux, et vice versa. Cela faisait pourtant des années que j'aurais dû comprendre : les bouquins remplis illusions d'optique m'avaient déjà préparé le terrain, en me montrant que certaines fois, mes sens me mentaient. Mais je n'avais jamais vraiment réfléchi au fait que cette règle s'appliquait même aux schémas les plus abstraits.
Les mathématiques, par exemple, n'étaient pas si parfaites que cela, elles étaient juste… réelles.
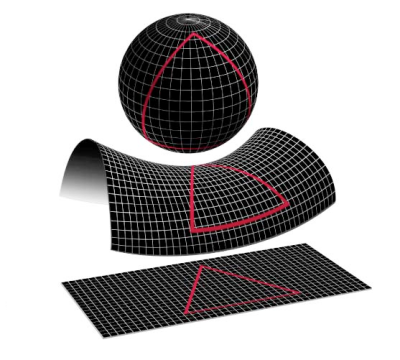
Crédit image : map Nasa
Même le sacro-saint théorème de Pythagore n'est pas complet ! Il ne s'applique que dans le cas d'un espace euclidien, plan. Qu'on courbe un peu la surface de travail, et la somme des angles ne vaut plus 180°, le théorème de Pythagore ne s'applique plus, et les distances que l'on calcule avec les coordonnées sont faussées (ce qui est logique, puisqu'elles dérivent d'une certaine façon du théorème de Pythagore).
En quelques secondes, ma vision simpliste des maths « parfaites » s'était transformée ; les maths étaient un édifice en construction, avec ses faiblesses, ses lacunes – mais où chacun pouvait participer. Chaque brique posée nous rapprochait d'un objectif inatteignable, et pourtant tellement désiré…
En fait, je comprenais enfin le théorème d'incomplétude de Gödel :
Il existe des énoncés sur lesquels on sait qu'on ne pourra jamais rien dire dans le cadre de la théorie.
Le seul moyen de progresser sera de créer une nouvelle théorie, plus puissante, qui englobe la première : tout comme mon crayon est sorti de la théorie des « 9 points dans un tableau de $3 \times 3$ », chaque chose est incomplète… tout en tendant vers son accomplissement, sans jamais l'atteindre entièrement.
Bouleversé par ma découverte, je n'avais pas remarqué qu'un vieillard était apparu à la porte. Alors que mes yeux se remettaient à fonctionner, après l'éblouissement par mon illumination, je remarquais une sorte de $\zeta$ brillant qui flottait à quelques centimètres de sa tête. Le vieil homme suivit mon regard, compris que je regardais la lettre grecque, et me sourit. C'était un sourire bienveillant, et plein d'affection. Lorsqu'il prit la parole, sa voix était douce et trahissait son érudition : « Rentrez, jeune homme. Je suis sûr que vous avez beaucoup de questions à me poser… ».
Pour en savoir plus : Théorème d'incomplétude de Gödel
À boire !
Subjugué par le charisme de cet homme, je le suivais et entrais dans sa maison. Sans surprise, tout à l'intérieur était géométrique et symétrique. Mais mon nouveau regard critique décelait les minuscules différences entre chaque côté, me prouvant à chaque instant la validité de mon nouveau mode de raisonnement. Le Supérieur m'introduisit dans son salon, et me proposa un siège.
« Cela faisait bien longtemps que je n'avais plus reçu de visites. Les intégrations à la maison des constantes se font rares, et les personnes qui réussissent à passer les embûches disséminées sur le chemin encore plus. Le jeune homme à ma fenêtre, coincé sur le chemin de la division par deux, en est la preuve vivante, et chaque matin, sa présence me rappelle que notre famille est en déclin. Nous vivons des heures bien sombres, si même nos héros ne triomphent pas des premières énigmes… $\Delta$, notre gardien, m'annonce souvent que les personnes qui échouent dès le problème de la balance sont légions… »
Je l'écoutais, subjugué par ses paroles. J'aurais voulu lui poser directement mes questions, mais une petite voix me disait qu'en le laissant parler, il répondrait tout seul.
« Tu comprends donc que ta présence éclaire mon cœur et mon visage. Je peux même sentir mon $\zeta$ briller ! », et effectivement, la petite lettre translucide qui flottait par dessus son visage semblait briller de mille feux, comme animée d'une volonté propre.
« Mais je parle, je parle, et je faillis à tous mes devoirs d'hôte ! Tu dois être assoiffé, après cette longue route… que veux-tu ? J'ai du coca, ou du whisky… »
Ah. Dilemme cornélien. Le coca aurait été rafraichissant, et nourrissant par son sucre. Quant au whisky, il m'aurait remis les idées en place… que choisir ?
Il dut percevoir mon hésitation, car il sortit d'un placard une bouteille de chaque, deux verres et une cuillère.
Il remplit à moitié chaque verre, le premier de coca et le second de whisky. Prenant sa cuillère, il la remplit de coca du premier verre, et la vida dans le verre d'alcool. Il mélangea alors ce dernier verre, avant d'en prendre une cuillère de contenu mixte, et de la vider dans le premier verre. Au final, chaque verre avait la même volume qu'au début… Le Supérieur releva ses yeux vers moi, l'air facétieux, et me demanda :
« A ton avis, y a-t-il plus de coca dans le whisky ou plus de whisky dans le coca ? Réfléchis bien avant de répondre… »
Solution no5
Instinctivement, j'aurais dit qu'il y avait plus de coca dans le whisky que l'inverse : après tout, il mettait une pleine cuillère de coca dans le whisky, alors qu'il ne mettait dans le coca qu'une partie d'une cuillère de whisky plus du coca. Mais depuis mon arrivée ici, je m'étais fait avoir trop souvent pour me fier sans réflexion à mon intuition…
Mon hôte me tendit un papier et un crayon… comme s'il avait lu dans mes pensées.
Posons tout cela à plat. J'appelais $c$ une unité de coca, et $w$ l'unité de whisky.
Arbitrairement, je pris une contenance de 200 ml pour chaque verre (donc 100 ml quand ils sont remplis à moitié), et 10 ml pour une cuillère (ce qui correspond donc à une “cuillère romaine” ), mais le raisonnement devait être le même dans tous les cas.
| Verre 1 | Verre 2 | Commentaire |
| $100 \times c$ | $100 \times w$ | À la première étape, les deux verres contiennent chacun 10 cl de chaque boisson. |
| $90 \times c$ | $100 \times w + 10 \times c$ | À la seconde étape, le vieil homme avait pris une cuillère du verre de coca (soit 10 ml de coca), et l'avait reportée dans le second verre. |
| $90 \times c$ | $(100 \times w + 10 \times c)_{melanges}$ | À la troisième étape, le Supérieur avait homogénéisé le contenu du verre. |
$90c + 10\frac{10w + c}{11}$ |
$100w + 10c - 10\frac{10w + c}{11}$ |
Voilà où les choses se corsent… |
$\frac{990c + 100w + 10c}{11}$ |
$\frac{1100w + 110c - 100w - 10c}{11}$ |
Il ne reste plus qu'à faire le calcul de fractions… |
Alors là ! J'en étais scotché… ainsi donc, les deux verres contenaient $\frac{1000}{11}$ de la boisson principale et $\frac{100}{11}$ de la seconde boisson… par acquit de conscience, je vérifiais que la somme des deux fractions donnait bien 100ml… c'était le cas.
Il y avait donc autant de coca dans le whisky que de whisky dans le coca… je choisis de prendre le premier verre de coca, celui qui contenait le plus de coca : cela m'aiderait à garder les idées claires pour la suite du récit, qui promettait d'être passionnante.
Pour aller plus loin
La solution donnée précédemment ne présentait pas un raisonnement très formel… mais avait le mérite d'être moins abstraite. Voyons tout de même le cas général, dans un souci de rigueur.
Un verre contiendra un volume $V$, une cuillère un volume $C$.
| Verre 1 | Verre 2 |
| $V \times c$ | $V \times w$ |
| $V \times c - C \times c$ | $V \times w + C \times c$ |
$(V-C)c + C\frac{Vw + Cc}{V + C}$ |
$Vw + Cc - C\frac{Vw+Cc}{V + C}$ |
| $= \frac{V^2}{V + C}c + \frac{CV}{V + C}w$ | $= \frac{V^2}{V + C}w + \frac{CV}{V + C}c$ |
Sans grosse surprise, on retrouve l'égalité… et en remplacant $C$ et $V$ par leurs valeurs respectives, on retrouve les résultats précédents
La grande diaspora
Mon hôte prit le second verre, en but une gorgée, et reprit son récit :
« Commençons par les choses qui fâchent : tout ce pays n'existe pas. Ou plutôt, il n'existe que dans vos têtes. Nous ne vivons que par le bon vouloir de votre civilisation, qui nous a imaginés, nourrie de ses rêves et des ses illusions. Chacun de nous n'est qu'une allégorie d'une notion d'un de vos penseurs… ça peut te paraître compliqué, voire même abstrait, mais en réalité, nous ne sommes rien de plus et rien de moins que votre imagination mathématique. Nous avons acquis notre nom avec les grecs, nos maisons avec les théories de l'arithmétique et les fonctions, qui en quelque sorte, nous prennent “en paramètre”, en hôtes. Notre paysage est dû à Descartes, qui a le premier établi un lien entre l'analyse et la géométrie. Quant à la structure de notre monde, elle est celle d'un sous espace vectoriel… comme te l'ont déjà appris tes précédentes rencontres. Jusqu'à récemment, nos deux mondes étaient complètement indépendants…
Ce n'est qu'avec l'avènement de l'analyse que nos deux mondes ont enfin pu communiquer. La possibilité de dériver et d'intégrer s'applique aux nombres, dons nous sommes les représentants… en conséquent, certaines équations peuvent nous amener provisoirement dans votre monde. Mais comme seule la personne qui manipule l'expression en est consciente, nous préférons dire que c'est elle qui est intégrée. Après tout, c'est un peu comme le principe des actions réciproques, mais appliqué à des nombres : si nous dérivons de ton point de vue, alors tu te fais intégrer pour nous. C'est logique… tordu, je te l'accorde, mais logique.
$\begin{bmatrix}Ici & -- &\\ & -- & Chez\,toi\end{bmatrix} \Leftrightarrow \begin{bmatrix}Ici & -- & \int Chez\,toi \\ \frac{\partial Ici}{\partial t} & -- & Chez\,toi\end{bmatrix}$
C'est de là que vient le nom de la maison où tu es arrivé, la maison des constantes. Comme tu le sais, lorsque l'on intègre, c'est à une constante près. Lors de ton arrivée, tu as donc reçu une constante… une sorte de don, qui t'a aidé dans la résolution des énigmes qui ont parsemées ton chemin. Elle brille d'ailleurs en ce moment même, au dessus de ta tête… »
Je levais immédiatement la tête, sans rien voir évidemment… puisque si elle était semblable à celle qu'avait le sage, elle bougeait avec mes mouvements de tête.
« Tu es bien conscient que tu n'aurais jamais pu trouver toutes ces réponses seules… ce don que tu reçois se manifeste plus ou moins fortement chez chacun, selon les conditions initiales que tu as fixées. »
« Attendez, attendez… tout ce que vous dites est peut être la vérité, dis-je en accentuant le peut-être, mais je n'en comprends pas la moitié ! Vous dites que c'est moi qui vous ait fait venir ? Et qu'est ce que c'est que ce charabia sur les conditions initiales ? »
Le Supérieur inspira profondément, comme s'il parlait à un enfant un peu lent à la détente… mais il le fit d'une façon qui montrait qu'il ne m'en voulait pas, ce dont je lui fût gré. Après tout, on ne se fait pas intégrer tous les jours, et je méritais un peu de compassion !
« Effectivement, tu nous a appelés, invoqués, convoqués : peu importe le terme… car tout dépend du point de vue : pour moi, c'est nous qui t'avons appelé ! Tout est réciproque et symétrique dans notre monde. Ta venue vient du fait que tu as résolu un problème, ou que tu as compris quelque chose d'important concernant les mathématiques, ou encore imaginé quelque chose de nouveau… bref, n'importe quoi en rapport avec notre monde abstrait. Alors tu t'es retrouvé ici… mais très peu de gens réfléchissent vraiment aux mathématiques. La plupart la considèrent juste comme une science à apprendre, et non comme une science à comprendre. C'est pourtant ce qui fait toute la différence… tu avais sûrement des prédispositions pour venir ici ! »
Je réfléchis un instant. Effectivement, j'avais toujours ressenti quelque chose de spécial en maths ; et je n'avais jamais appris une seule formule dans cette matière. Après tout, il était si intuitif de les retrouver ! Je commençais à voir où il voulait en venir.
« Mais même parmi ces penseurs, votre qualité n'est pas toujours la même. Certains d'entre vous sont meilleurs dans des domaines précis… et mauvais partout ailleurs. D'autres personnes échouent avant même de commencer – comme cet homme devant ma porte, toujours plus proche mais paradoxalement plus loin de moi…
Pour être franc, nous n'avons très peu de visiteurs, même selon nos critères de temps. Mais chacun d'entre eux nous marque de son passage. Et nous les marquons de la même façon, toujours dans cette même relation d'équilibre. L'un de nos derniers visiteurs s'est ainsi senti forcer de nommer une fonction de son invention par mon nom. Une fonction nommée Zeta ! Quelle idiotie ! Mais je ne peux pas lui en vouloir… et je suis flatté de voir que même aujourd'hui, son hypothèse concernant cette fonction n'est ni démontrée, ni comprise. Cela prouve que notre pays peut encore être amélioré. Je me demande bien ce qui sortira de tout cela ! », finit-il, l'air curieux.
« Mais… d'où venez-vous ? Vous ne pouvez pas apparaître comme ça ! Ce n'est pas parce que Descartes a lié les nombres et la géométrie que ce terrain est apparu ! Il devait être quelque part avant ‽ »
Il me sourit.
« Tu comprends vite… nous venons tous d'un lieu, le grand Néant, où tout ce qui pourrait être inventé se trouve sous forme brute : des amas noirs qui ne ressemblent à rien – jusqu'à ce qu'on les mettent en lumière. Mais je n'ai pas le droit de t'en dire plus… pour ne pas t'influencer. Tu imagines si tu savais à l'avance ce que tu devais découvrir ? Ce ne serait plus une vraie découverte ! »
Je comprenais. De toute façon, j'aurais eu horreur qu'on me prémâche le travail.
« Et combien êtes-vous à vivre dans ce sous espace vectoriel ? »
« Encore une fois, une très bonne question, à laquelle je vais répondre par une autre question, qui nécessite un gros flashback.
À l'origine, nous étions donc tous dans le grand néant, lorsqu'un jour “on” nous convoqua tous… “on” nous informa que certains d'entre nous allaient être marqués pour participer à l'une des plus grandes odyssées. Ceux d'entre nous qui devaient émigrer vers cette terre promise seraient marqués d'une lettre au dessus de leurs visages. Cette lettre serait invisible pour nous, mais tous les autres pourraient la voir. La règle était simple : tout les “jours” – je dis jours, mais ce n'étaient pas des jours au sens où tu le conçois… mais qu'importe, si cela t'aide à comprendre le problème – les entités qui se savaient marquées devaient voyager vers notre nouvel habitat. Le problème, c'était que nous ne pouvions pas savoir si nous étions marqués et qu'on ne pouvait pas nous le dire, puisque le grand néant n'a pas de structure pour supporter les sens et en particulier, les sons. Nous pouvions juste sentir au plus profond de nous mêmes les personnes qui étaient marquées… sans pouvoir en déduire une quelconque information nous concernant. Heureusement, “on” nous donna une indication qui nous permit de nous en sortir : nous étions au moins deux à être marqués. Rien ne se passa pendant 24 jours… et au matin du 25ème jour, tous ceux qui étaient marqués prirent le portail. Je te laisse deviner combien nous étions… »
J'avais dépassé le stade de l'incompréhension. Je nageais en pleine science fiction… mais je fis tout de même un effort pour résumer ce qu'il venait de me dire :
« Donc, si je me mets dans la peau de l'un des vôtres, voilà ce que je sais :
Dans notre population isolée, un certain nombre d'entre nous (disons $n$) sont marqués d'un sceau. Au jour $j=0$, je sais qu'au moins deux personnes sont marquées… mais je ne sais pas moi même si je suis marqué… et je n'ai aucune façon de l'apprendre par les autres habitants. En revanche, si je venais à apprendre que j'étais marqué, je devrais voyager au matin. Et comme par magie, à l'aube du 25ème jour ($j=25$), tous les marqués partent ! Aucun n'est parti avant… mais quel rapport ? Pourquoi 25 jours ? »
Ainsi soliloquais-je tandis que le Supérieur finissait son verre de whisky, les yeux dans le vague, comme plongés dans des souvenirs datant de plusieurs millénaires…
Solution no6
Plus j'y réfléchissais, moins je comprenais. Son récit m'avait déjà embrouillé l'esprit, alors réfléchir à un problème de ce type… Je ne voyais vraiment pas le rapport entre les 25 jours et le départ de ces… entités. Pourquoi ne s'était-il rien passé avant ? Et lui qui continuait de siroter son whisky ! Je remarquais d'un œil discret qu'il tenait son verre de la main gauche. C'était intéressant, car d'habitude je ne faisais jamais attention à ce genre de détails. Mais peut-être n'était-ce pas un détail ! J'avais lu quelque part que les gauchers, confrontés à un problème, ont tendance à essayer de le résoudre par synthèse, c'est à dire en considérant le problème comme un tout, et en tentant de le résoudre « de l'extérieur ». C'était exactement ce que j'étais en train de faire… inversement, les droitiers résolvaient le problème par analyse, en le divisant en plusieurs petits problèmes. Sur le coup, j'avais pensé que cette distinction entre les deux latéralités était stupide, mais pourquoi ne pas tenter d'appliquer la méthode d'analyse à mon problème actuel ? Après tout, je n'avais rien à perdre !
Voyons voir… pour simplifier, imaginons qu'il n'y ait que 2 nominés pour l'exil.
Dans ce cas là, tous les autres voient deux personnes marquées… mais ils ne peuvent rien en déduire pour eux-mêmes. En revanche, ceux qui sont marqués ne voient qu'une seule personne, et comme ils savent qu'ils sont au moins deux, ils peuvent en déduire leurs états. Et ils partiraient donc au matin du 1er jour, à deux.
Bon, j'avais résolu mon premier petit problème. Comment m'en servir pour avancer ?
Disons maintenant qu'il y ait eu, non plus deux, mais trois marqués. Dans ce cas là, le premier jour, chacun des marqués voit deux personnes marquées… et ne sait donc pas qu'il est marqué. En revanche, il se dit que les deux marqués qu'il voit vont appliquer le raisonnement vu précédemment, c'est à dire qu'ils vont partir au matin du premier jour. Mais le lendemain, catastrophe ! Ils ne sont pas partis… déduction logique : chacun d'eux voyait deux marques et pensaient que ces deux marqués appliqueraient le raisonnement décrit plus haut. Et ils peuvent alors comprendre qu'eux aussi sont marqués (par empathie, en réfléchissant à la place des autres) : dans ce cas là, au matin du second jour, les trois partiraient.
Le même raisonnement s'appliquait si $n=4$ : chacun voit trois personnes de marquées, et se ramenant au cas précédent, imagine qu'ils quitteront les lieux au matin du second jour. Comme ils ne partent pas ce jour là, c'est forcément qu'il y a un marqué de plus… soi même, en l'occurrence. Et chacun d'eux partira donc au matin du troisième jour.
En appliquant ce raisonnement de façon récurrente, on obtenait :
$\begin{Bmatrix}j & & n \\ 1 & \mapsto & 2 \\ 2 & \mapsto & 3 \\ 3 & \mapsto & 4 \\ & \vdots & \\ j & \mapsto & j+1 \\ & \vdots & \\ 25 & \mapsto & 26\end{Bmatrix}$
Et au bilan, si tout le monde partait le 25ème jour, c'est que 26 personnes étaient marquées à l'origine. Plutôt fier de mon raisonnement, j'expliquai ma démarche et mes conclusions au Supérieur. Celui ci me fit un petit sourire… mais je continuais cependant de parler :
« Cela dit, il aurait suffit qu'une seule personne ne se place pas dans la peau des autres, ou ne réfléchisse pas de la même façon, pour que l'ensemble de l'édifice s'effondre. Ce problème n'est soluble qu'en admettant une capacité d'empathie très forte entre chacun. Et il faut aussi admettre que vous étiez tous extrêmement intelligents… »
Il eut l'air déçu de ma remarque : « N'as tu pas encore compris ? Tes notions humaines d'intelligence ou d'empathie ne s'appliquent pas à nous ! As-tu déjà vu un nombre souffrir ? Ou une constante qui réfléchissait ? En revanche, chacun de nous est à la fois similaire et différent de tous les autres, et nous formons un tout plus cohérent que ta civilisation… ce qui explique pourquoi pour nous, ce problème était… trivial. Et cela explique aussi pourquoi tu dois partir. »
Mise en boite
Partir ?
À mon arrivée, cela avait été mon plus cher désir. Maintenant… je ne savais plus ce que je voulais. J'avais perdu amis et famille, et j'avais gagné une capacité surhumaine de réflexion et d'intelligence.
Mais à quoi tout cela me servirait-il si je ne pouvais en faire profiter personne ? Dans ce pays, je ne pouvais qu'apprendre, un apprentissage non réciproque : tout ce que je savais sur les sciences, ils le savaient mieux que moi ; et toutes mes autres connaissances m'étaient inutiles ici, dans ce pays gouverné par les mathématiques.
Alors que chez moi, je pourrais profiter de mes nouvelles capacités… soudain, je réalisais que je devais absolument rentrer. Même si ce pays était magnifique et parfait, il était paradoxalement insupportable. C'était un pays trop carré, où le libre arbitre et les choix n'avaient pas lieu. La vie ici n'était que la résolution d'une équation entièrement fixée ne laissant aucune place au hasard, le destin de chaque être inscrit dans des chiffres comme la vie d'un saint dans une hagiographie : parfaite et sans fioritures – trop belle pour être vraie, trop triste pour être vécue. Mais pour rentrer chez moi, il me faudrait dériver… et perdre mes capacités nouvellement acquises.
Mon hôte dût remarquer mon air interrogateur, puisqu'il répondit à ma question implicite :
« Tu perdras la capacité à raisonner que tu as acquise ici… mais tout ce que tu as appris et compris restera. C'est pour cela que nous poussons nos visiteurs à réfléchir : tout ce qu'ils comprennent rapidement ici, il leur faudrait plusieurs années pour l'apprécier réellement dans leurs mondes. Depuis ton intégration, je suis sûr que tu as appris et compris une foule de choses nouvelles : tu as su imaginer une nouvelle solution à un problème antédiluvien avec la balance, tu as su raisonner avec les mathématiques pour le problème de l'héritage des trois frères, tu as fait preuve d'inspiration en évitant le chemin infini, tu as su sortir du cadre théorique que tu t'imposais inconsciemment en venant à bout de ma serrure, tu as réussi à ne pas te fier directement à ton intuition mais plutôt à faire confiance aux nombres pour le problème de la boisson, et récemment tu as montré que tu étais capable de subdiviser un problème pour mieux le résoudre. Alors certes, il te reste quelques petites choses à découvrir, mais dans l'ensemble, ton raisonnement déjà hors-normes a été boosté par ton rapide séjour ici. Et ce n'est pas fini… si tu veux partir, il te faudra la clé de la maison des constantes, car elle s'est refermée derrière toi. Et comme tu t'en doutes, je ne vais pas te donner cette clé directement… »
Sur ces paroles, il sortit d'un placard trois boites en bois, toutes semblables.
« L'une de ces boites contient la clé de la maison… les deux autres sont vides.
Désigne-moi une boite au hasard… tu as une chance sur trois de trouver la clé ! »
N'ayant aucun repère, je choisis aléatoirement la boite de gauche. À ma surprise, il ouvrit la boite du milieu… et me montra son contenu : elle était vide. Il reprit :
« Sachant que cette boite est vide, souhaites-tu changer d'opinion ? »
Solution no7
À première vue, le fait de changer de boites n'apportait rien : j'avais autant de chances de trouver juste du premier coup que du second coup, puisque la clé n'avait pas bougée entre les deux étapes : dans tous les cas, j'avais une chance sur deux de trouver la clé.
Et pourtant, une petite voix à l'intérieur me criait que je faisais une erreur. En ouvrant la boite, Zeta ne m'avait donné aucune information : lui savait déjà où se trouvait la clé ! Je pouvais donc simplifier l'énoncé de son problème de cette façon : je choisis une boite (appelons là A, et les deux autres B et C), et ensuite, je peux choisir de prendre toutes les autres boites sauf celle que j'ai sélectionnée en premier : en effet, toutes ces autre boites correspondent à B et C, où B n'est plus une inconnue puisque ouverte. Dans un cas, j'ai une chance sur trois de réussir, dans l'autre deux chances sur trois !
Je commençais à y voir plus clair, et de deux choses l'une :
- Soit j'avais choisi la bonne boite, (une chance sur trois), et si je changeais, je perdais.
- Soit j'avais choisi la mauvaise boite (deux chances sur trois) : en changeant d'opinion, je gagnais !
En exagérant, on pourrait dire que le problème revenait à avoir 1000 boites, que j'en choisisse une parmi ces mille boites (probabilité de $\frac{1}{1000}$ de tomber juste), puis que le Supérieur m'ouvre 998 boites toutes vides : en changeant de choix et en désignant la dernière boite restante (mise à part celle désignée en premier lieu), la probabilité de trouver la clé devenait $1-\frac{1}{1000}=\frac{999}{1000}$
Cette fois, encore plus que d'habitude, mon intuition m'aurait trompé : sans y réfléchir, j'aurais pu faire un mauvais choix. Mais même en réfléchissant, il me restait une chance sur trois de me tromper… on n'a rien sans rien, pensais-je, en indiquant la troisième boite.
Il eut un petit sourire, et ouvrit la boite de droite… qui était vide.
« Vois-tu, logique et réflexion ne peuvent pas te sortir seules de toutes les situations. Tu n'auras jamais un contrôle total sur tout ce que tu manipules : il y aura en permanence des inconnues que tu ne peux déterminer. Il te faudra alors composer avec ces inconnues… et non les ignorer. Ton but est de faire de ton mieux, même dans les cas où le mieux n'est pas grand chose. Et si tu devais échouer, reste humble, et ne t'enfonce pas dans la spirale des remords. J'espère que cette petite expérience te servira de leçon. Mais ne le prends pas mal : tu n'avais aucun moyen de prévoir ce retournement ! Va maintenant, tu trouveras un autre moyen pour rentrer dans la maison des constantes… mais je crois savoir que certaines énigmes t'attendent encore sur le chemin. Pars donc affronter ton destin… et à ton retour chez les tiens, souviens-toi de tout ce que tu as appris ici. »
Pour en savoir plus : Le problème des trois portes
Prise de mouche
Après quelques adieux, $\zeta$ me confia un bloc de papier et un crayon, me disant d'un ton énigmatique que j'en aurais besoin pour la suite. Je le remerciais, à la fois pour ce don et pour toutes les connaissances qu'il m'avait enseigné, et sortai de chez lui par la porte de derrière, prêt à retourner dans mon monde. Alors que j'atteignais le portillon qui me ramènerait sur la route, le Supérieur me héla une dernière fois :
« Tu vois l'homme là bas, à l'autre bout de la route, sur le chemin qui te ramènera à la maison des constantes ? Il est à une distance de deux kilomètres. Il est sur son vélo, et partira vers toi au moment où tu feras ton premier pas sur la route. Sur son guidon, une mouche s'envolera au moment de son départ. Cette mouche volera à une vitesse constante vers toi, et au moment ou elle t'atteindra, elle fera demi-tour vers le cycliste (sans perte de vitesse). Dès qu'elle reviendra au cycliste, elle repartira vers toi… et ainsi de suite, jusqu'à ce que le cycliste et toi vous croisiez.
$\begin{matrix}Cycliste & \leftarrow 2km \rightarrow & Moi \\ \longrightarrow & \cdots \cdots \cdots & \longleftarrow\end{matrix}$
À ce moment, le cycliste, qui est aussi notre videur dans ce monde, te demandera combien de kilomètres a parcouru la mouche. Si tu réponds mal, il t'éliminera purement et simplement du sous ensemble vectoriel… et tu te retrouveras dans le grand néant. Si tu réponds bien, en revanche, il te laissera passer, et tu pourras retourner à la maison des constantes. Oh, et j'allais oublier : tu trouveras les vitesses de chacun de vous sur ton premier feuillet… »
Effectivement, la première page du bloc de papier contenait les inscriptions suivantes :
- Toi : $5 km.h^{-1}$
- Cycliste : $25 km.h^{-1}$
- Mouche : $120 km.h^{-1}$
Ça c'est de la mouche supersonique ! J'aurais cru qu'une mouche ne dépassait pas les 10km/h, mais après tout, dans ce monde où les mouches savaient résoudre des équations différentielles du septième degré, rien ne m'étonnait plus… et je n'avais aucune envie d'être désintégré ( !) dans le grand néant. Je commençais donc à marcher, tout en griffonnant frénétiquement des équations sur mon papier…
Solution no8
Plus j'approchais, plus l'angoisse me saisissait. Je remplissais des pages et des pages d'équations complexes, chaque côté de l'équation variant avec le temps selon des inconnues difficilement maîtrisables. Je n'avais aucune envie d'échouer si près du but, alors que je venais de comprendre le concept de ce lieu… il me restait tellement de choses à faire, et le temps dont je manquai n'était qu'à une réponse de cette équation… il me suffisait de résoudre ce système pour gagner ma liberté et mon avenir ! Je devai réussir, je ne devai pas penser aux enjeux… me concentrer sur le problème, chaque chose en son temps !
La distance entre nos deux personnes diminuait dangereusement. Je voyais la mouche qui s'évertuait à effectuer ses allers-retours, de distances toujours plus courtes… et lui toujours plus près… arriva alors le moment fatidique, celui ou le videur s'arrêta juste devant moi avant de me regarder d'un air interrogateur.
Je n'avais aucune réponse à lui fournir. Et aucune envie de finir dans le grand néant ! Je tentais donc l'approche « se faire passer pour plus bête que l'on n'est » :
« Déjà ? Mais cela ne fait que quelques minutes… je n'ai pas eu vraiment le temps… »
Inconsciemment, je calculais avec les valeurs que j'avais : il y avait deux kilomètres, nous avions marché à une vitesse cumulée de $25 + 5 = 30 km.h^{-1}$ : j'avais donc disposé d'un quinzième d'heure pour résoudre mon problème, soit 4 minutes…
Une porte s'ouvrit alors avec fracas dans mon esprit : je tenais une nouvelle fois l'illumination ! Souriant, je jetai au vent les brouillons usagés (il est peu probable que les habitants d'un sous ensemble vectoriel se soucient de pollution et d'écologie), et annonçai avec un grand sourire au videur que notre mouche boostée à la testostérone avait parcourue la distance de 8km.
L'homme me regarda sans dire un mot, avant de renfourcher son vélo et de s'en aller, sa mouche à l'épaule.
Je me retournais vers lui, et criais d'un ton moqueur :
« Et heureusement que nous sommes dans un pays virtuel ! Parce que sinon, ta mouche, elle subirait une accélération infinie lors de son demi-tour ! Dans mon monde, on n'en récupérerait même pas du pâté de mouche… »
Il ne daigna pas renchérir, ou peut-être n'entendit-il pas.
Toujours est-il que je repris mon chemin l'air joyeux, n'en revenant pas de mon récent acte de bravoure – et en quelque sorte, de rébellion contre l'autorité locale). Revenons sur mon raisonnement.
J'aurais certes pu répondre au problème par la méthode analytique, en résolvant les équations, mais j'avais trouvé une méthode bien plus simple.
À nous deux, nous parcourions 30 kilomètres en une heure. Autrement dit, il nous avait fallu 4 minutes pour nous rencontrer sur ce trajet de deux kilomètres.
Peut importait le nombre d'allers retours effectués par la mouche : ce qui comptait, c'est que comme nous, elle avait eu un temps de déplacement de 4 minutes. Et en 4 minutes (soit $\frac{1}{15}$ d'heure), à 120 km/h, on parcourt $120 \times \frac{1}{15 } = 8km$.
J'aurais pu m'enfoncer dans un raisonnement extrêmement complexe, alors qu'il suffisait de changer de point de vue et de réfléchir autrement pour comprendre. J'aurais pourtant dû finir par apprendre cette leçon !
Grab me a child of 5 !
Encore tout fier de ma récente répartie, j'arrivais devant la maison des constantes. À première vue, rien n'y avait changé ; mais c'était à première vue seulement. Car la porte par laquelle j'étais sorti était maintenant fermée… je craignais d'y trouver une serrure dont la clé me manquait, mais je n'eus pas à m'inquiéter pour cela : la porte était simplement fermée par un digicode – de forme assez spéciale.
$\begin{matrix}21\\ \begin{bmatrix}+ & - && \times \\ \\ 1 & 5 & &\div \\ 6 & 7 & & = \\ ( & )\end{bmatrix}\end{matrix}$
Après quelques tâtonnements, je finis par comprendre les principes de cette serrure assez spéciale :
- Je pouvais utiliser une seule fois chacun de chiffres ;
- Je pouvais utiliser autant de fois que je voulais chaque opération élémentaire ;
- Je devais forcément alterner chiffres et signes : je ne pouvais donc pas marquer 1, puis 5 pour faire un 15 ;
- En appuyant sur la touche $=$, le digicode effectuait la ligne de calcul, et vu le chiffre au dessus, j'en déduisis qu'il ne s'ouvrirait que si le total faisait 21.
Je commençais rapidement à tâtonner : $7 \times ( 5 - 1) - 6 = 7 \times 4 - 6 = 22$.
Ça ne passait pas loin ! Je n'en aurais pas pour plus d'une minute, et déjà, je me prenais pour un candidat des chiffres et des lettres : « le compte est bon, mon cher ! »…
J'étais presque déçu : c'était tout ce qu'ils avaient trouvé ? Ils croyaient vraiment que cela allait me bloquer, moi, l'Élu de ce monde ? Alors que de leur propre aveu, j'étais génial ? Je me sentais vexé qu'ils me pensent incapable de résoudre une simple ligne de calcul, après toutes les démonstrations de mon talent dans ce monde ! Pour qui me prenait-on ? Un collégien ? Un lycéen attardé ? Quelle honte ! Quelle infamie… j'en aurais mordu quelqu'un, si je n'avais pas eu peur de recracher des décimales…
Solution no9
Une demi-heure passa, puis une heure… je testais inlassablement des combinaisons de nombres, à la recherche d'un hypothétique 21…
Si j'avais été sur Terre, le soleil se serait couché, et m'aurait fait comprendre qu'il était plus que temps de me reposer, afin de prendre un peu de recul. Mais dans ce lieu, la lumière provenait toujours du même point, à la même intensité, fixe et immuable comme une constante mathématique, et je n'avais aucun moyen d'estimer le temps qui passait. J'avais commencé par essayer de trouver un 3 avec 1, 5 et 6, pour multiplier ce 3 avec le 7 et obtenir 21, mais toutes mes expérimentations en ce sens s'étaient révélées vaines. J'obtenais 22 de différentes façons, mais jamais 21… mon cerveau fatigant m'envoyait des signaux d'alarme, mais je n'en tenais pas compte et persévérait dans ma vaine entreprise.
Finalement, la fatigue eut raison de moi, et je m'endormis au pied de la porte, d'un sommeil peuplé de rêves étranges dans lesquels des 21 voletaient autour de moi sans jamais se laisser attraper.
À mon réveil, j'avais acquis la conviction que cette énigme était impossible.
Cette conviction se basait sur le fait que mes recherches étaient restées vaines, alors que mon intellect supérieur aurait dû trouver la solution si elle existait. Bon sang, un collégien aurait trouvé la solution si elle existait ! Il n'y avait pas des milliards de possibilités, après tout : quatre chiffres, quatre opérations… si la solution existait, je l'aurais trouvée ! J'avais testé des centaines de possibilités, pour toujours tomber sur des nombres différents de 21.
Si seulement on avait pu utiliser des racines carrées, ou des puissances ! Je n'aurais eu qu'à marquer $\frac{6 \times 7}{\sqrt{5-1}} = 21$ ! Mais non, il fallait que je restreigne mon génie aux quatre opérations de base, les opérations utilisées par les profanes qui ne connaissent rien aux mathématiques ! De rage, je donnais un violent coup de poing au digicode, qui ne m'opposa qu'un faible bip…
« Ce n'est pas de cette façon que tu trouveras la solution, tu sais… »
Surpris, je fis volte face pour me retrouver face aux trois frères que j'avais aidés à mon arrivée. Ils avaient changé de vêtements, mais c'était bien eux…
« Cette énigme est impossible ! On essaie de me bloquer ! De me faire passer pour un fou ! Il est impossible de sortir de ce pays ! Cette serrure est inviolable… pourquoi ? Pourquoi ? »
Je crois que j'avais dépassé les bornes de la colère. Je me sentais frustré d'échouer sur une énigme aussi simple, fatigué par mes recherches… il me semble qu'ils me proposèrent leur aide, mais je la déclinais de façon fort peu polie, leur rappelant qu'ils étaient déjà incapables de résoudre leurs petits problèmes familiaux. Ils me laissèrent donc, et je perdis de nouveau plusieurs heures à manipuler ces 4 chiffres. Je me décidais pour une approche plus méthodique, et remplit des pages et des pages de formules.
En tournant l'avant dernière feuille, je trouvais un message que le Supérieur avait dû griffonner à mon insu :
« Même les plus grands génies ont besoin d'aide. »
Alors que je cherchais si cette phrase sibylline ne dissimulait pas un indice, une voix retentit à mes côtés : c'était le plus âgé des trois frères, qui était revenu me voir.
« Le vieux fou n'a pas tort… tu sais, si tu passes trop de temps sur quelque chose, tu finis par te focaliser sur le problème, et plus sur la solution. Tu devrais toujours accueillir avec joie un nouveau point de vue, et encore plus s'il est radicalement différent du tien. C'est cette ouverture d'esprit qui fait avancer la science ! Regarde l'étendue de vos connaissances scientifique : chacun y a apporté sa petite pierre, et vous avez réussi à construire un bel édifice. Maintenant, imagine ce qui se passerait si chacun avait tenté de bâtir dans son coin : vous ne construiriez que des huttes de paille ! L'union fait la force, tu devrais le savoir. Et pourtant, tu nous as rejetés, tu nous as sous-estimés… tu as pêché par orgueil, et tu as attrapé ce qu'on appelle couramment la grosse tête. Regarde tes dernières réactions ! Tu te moques de notre videur alors que tu as échappé in extremis à sa sanction, tu t'imagines plus intelligent que n'importe qui en te sentant insulté par une énigme aussi “simple” , et tu dénigres les autres sous le simple prétexte qu'ils ont échoués une fois.
Tu sais, en maths, on parle de transitivité : si on a $a < b $ et $ b < c$, on a forcément $a < c$.
Les humains ne sont heureusement pas pareils ! Regarde les compétitions sportives : ce n'est pas parce qu'un joueur B bat un joueur A et que le même joueur B est battu par C que C battra A ! Vous avez même un jeu qui illustre parfaitement cette notion : chifoumi. Choisir la pierre, la feuille ou les ciseaux n'influe pas du tout sur les probabilités de gagner : les ciseaux perdent contre la pierre, la pierre perd contre la feuille, et la feuille perd contre les ciseaux, qui perdent contre la pierre, et cætera.
En résumé, ta prétendue supériorité est peut-être avérée, mais ce n'est pas une raison pour mépriser les autres… après tout, on a toujours besoin d'un plus petit que soi ! »
Dans ma tête s'agitaient des pensées contradictoires, mais l'une d'elles prit l'aval : c'était la honte de mes dernières actions. J'avais effectivement agi comme un monstre, et s'il ne me l'avait pas fait remarquer, je me serais enfoncé dans cet état d'esprit dénué de toute humilité. Tout ce qu'il avait dit était la vérité, et j'étais un imbécile de ne pas avoir vu cela par moi même. Je lui fis part ce cette dernière remarque, à laquelle il répondit par un simple « il ne faut pas non plus tomber dans l'excès inverse ». Nous rîmes en choeur, puis il reprit son sérieux :
« Je suis heureux d'avoir pu te raisonner, et fier de t'avoir connu… maintenant, voilà un indice qui devrait t'aider pour tes problèmes actuels : c'est un proverbe. Il dit de diviser pour mieux régner ; je te laisse en tirer les conclusions qui s'imposent ! Bon retour parmi les tiens, jeune homme. Je te souhaite un avenir brillant. Mais n'oublie rien de ce que tu as appris ici, que ce soient les énigmes ou les expériences humaines. »
Je le regardais descendre la route, en réfléchissant à ses dernières paroles. Diviser pour mieux régner… que devais-je comprendre ? Jusqu'ici, j'avais instinctivement évité les fractions, mais peut-être manquais-je quelque chose ? Mais les nombres que je manipulais étaient trop petits pour nécessiter une division ! Une petite voix criait dans mon esprit la solution, mais je n'arrivais pas encore à la saisir. Jusqu'à ce que je comprenne le proverbe.
Diviser pour mieux régner.
En coupant, on obtient plus.
Tout comme en divisant par un nombre inférieur à 1, on obtient plus que ce qu'on avait au départ…
Mais je n'avais pas de nombres inférieurs à 1 ! Il me fallait donc en créer… après plusieurs tâtonnements, je finis cependant par résoudre le problème, et le marquer sur le digicode :
$\frac{6}{1-\frac57} = 21$
J'en aurais pleuré de bonheur. C'était à la fois si simple… et si insaisissable ! La petite voix à l'intérieur de ma tête me soufflait que seul un vrai génie aurait pu trouver cette solution, mais je la fis taire : j'avais trouvé grâce à l'aide de mon nouvel ami. Et je retiendrais les deux leçons que je venais d'apprendre à la dure.
C'est sur ces bonnes pensées que je pénétrais dans la pièce aux murs blancs qui m'avait accueillie quelques « jours » plus tôt, à une époque où j'étais encore un individu lambda. J'eus alors la certitude que c'était cette lettre qui me planait au dessus de la tête et qui m'avait accompagnée pendant tout mon périple. J'aimais bien ce symbole… et je me sentais fier d'en être totemisé de cette façon.
Sur la table trônait toujours la balance, vidée de ses billes…
J'étais revenu à mon point de départ…
J'allais enfin rentrer chez moi !
J'étendis les bras, fermant les yeux, attendant avec impatience de sentir une quelconque preuve de mon retour.
Un dernier problème
Après quelques minutes dans cette position ridicule, alors que je commençais à me poser des questions sur la possibilité d'un retour de cette façon, je sentis comme une ombre qui me passait sur le visage.
Ça y est ! J'étais revenu ! Débordant d'enthousiasme, j'ouvris les yeux… et me retrouvais face à face avec l'homme qui m'avait “accueilli” à mon arrivée, et que le Supérieur avait nommé Delta.
« Et bah alors ? On dort ? En tout cas, tu avais l'air ridicule, permets moi de te le dire ! Mais passons ! $\zeta$ m'a dit que tu souhaitais rentrer… ça va bien faire trois cycles que je t'attends ! Tu t'es perdu en chemin ? »
Voyant que je ne répondais pas, il rit de sa propre blague, sachant pertinemment pourquoi j'étais en retard : à cause du digicode.
« Enfin bref, pour rentrer chez toi, il va te falloir résoudre une dernière énigme. La première utilisait une balance, la dernière de même. Mais cette fois, il va te falloir faire preuve d'un peu plus de subtilité… parce qu'en toute sincérité, le premier problème de la balance n'est qu'un test édulcorant pour éviter d'accueillir tous les pouilleux de votre monde. Et le dernier vise à conserver au maximum nos visiteurs. On a d'ailleurs un type qui n'avait pas su résoudre cette énigme et qui est mort récemment, bloqué dans ce pays… en laissant un testament bizarre à ses trois gamins. Toujours est-il que cet homme avait réussi toutes les épreuves précédents avec brio, mais qu'il n'a jamais réussi à franchir cette étape. Oh, pour être franc, je crois qu'il a arrêté de chercher après quelques mois, et qu'il s'est fait à l'idée qu'il lui faudrait désormais vivre ici. Et si tu veux mon avis, tu bloqueras aussi.
Mais assez monologué ! Voilà le problème. »
Je ne lui dis pas que j'avais déjà résolu le problème du testament, et me contentais de le regarder d'un air inexpressif, tandis qu'il sortait de sa poche un sac de billes qui ressemblait curieusement à celui qu'il m'avait tendu à mon arrivée ; sauf que ce sac contenait beaucoup moins de billes.
Toujours silencieux, j'attendis la suite des instructions… qui ne tarda pas :
« Ce sac contient douze billes, toutes numérotées, dont l'une est de poids différent des autres (soit subtilement plus légère, soit subtilement plus lourde). Tu vas devoir, en trois pesées, déterminer la bille différente, et la mettre dans la borne d'intégration à gauche de la balance. Puis, si tu estimes que cette bille est plus légère, tu presseras le signe $+$, et sinon, tu appuieras sur le bouton $-$. Si tu réussis, tu te retrouveras dans ton monde. Si tu échoues… je pense que tu ne veux pas savoir ce qui se passera si tu échoues.
N'oublie pas : trois pesées ! Et tu ne sais pas si la différence de masse est positive ou négative… »
Solution no10
Si on pouvait déterminer la bonne bille parmi 80 en 4 pesées, il n'y aurait sûrement pas de problèmes avec 12.
Sauf que ! Dans ce cas là, je ne savais pas si la bille était plus lourde ou plus légère. Et cela changeait tout ! Plongé dans mes réflexions, je contemplais les douze billes, chacune d'entre elles portant une lettre entre $a$ et $l$.
Je m'imaginais réappliquant la méthode de la trichotomie.
Première pesée, 4 sur chaque plateau et 4 en dehors. Imaginons que cela penche à droite… me voilà bien avancé. Comment pourrais-je alors savoir s'il y avait une bille plus légère à droite, ou une bille plus lourde à gauche ? Et bien évidemment, je n'avais aucune envie de laisser mon destin au hasard !
J'essayais ainsi mentalement plusieurs combinaisons, mais à la troisième pesée, il me restait toujours au moins deux billes, soit l'une plus lourde que l'autre, soit l'autre plus légère que l'une. Et aucun moyen de trancher !
Une idée revenait inlassablement me distraire : je devais quitter ce sous ensemble vectoriel. J'en revenais à la définition d'un sous ensemble vectoriel, laissant mon esprit vagabonder sur les différentes notions qui surgissaient, liées à ce mot. Algèbre linéaire. Matrices. Applications linéaires. Norme. Produit scalaire. Combinaison linéaire. Combinaison linéaire ? Mais oui !
Chaque bille était en quelque sorte une variable, et je devais faire en sorte d'optimiser chacune de mes équations, en évitant la redondance d'information. Pratiquement, cela signifiait que si ma première pesée contenait dans une balance les billes $a et b$, alors une seconde pesée devrait les séparer : sinon je n'aurais que des informations concernant l'ensemble $a et b$, et aucune information concernant $a$ et $b$ pris séparément.
De la même façon, laisser pour les trois pesées une bille dans le “troisième plateau” (en dehors de la balance) ne me permettrait pas de savoir si elle était plus légère ou plus lourde que les autres.
J'avançais un peu en saisissant cette astuce, mais je restais tout de même dans le brouillard.
Je décidais de réappliquer la méthode d'analyse (résoudre un problème en le coupant en problèmes plus simples), et me concentrais sur la première pesée. Sans prendre de risques, et sans pertes de généralité, je pouvais affirmer que j'allais peser $abcd$ dans le premier plateau, $efgh$ dans le second, et $ijkl$ en dehors.
Je décidais de m'avancer un peu plus, en supposant que ma deuxième pesée ne tiendrait pas compte du résultat de la première, et que cette pesée appliquerait au maximum le principe de dispersion décrit plus haut : deux billes dans le même plateau à la première pesée serait séparées (dans la limite du possible) pour la seconde pesée.
Autrement dit, pour disperser l'ensemble $abcd$, je mettrais $a$ dans le premier plateau, $b$ dans le second, et je serais forcé de mettre $cd$ dans le troisième plateau. (le troisième plateau désignant, comme dit plus haut, les billes qui ne sont pas pesées).
Je disperserais de la même façon le paquet $efgh$ : $e$ dans le premier plateau, $f$ dans le second, et $gh$ dans le troisième. Mais dans ce cas là, mon troisième plateau (de la deuxième pesée) serait plein (car j'avais déjà mis $cd$ dedans), et je ne pourrais pas disperser $ijkl$ (le troisième plateau de la première pesée) de façon convenable. Je préférais donc disperser ce deuxième plateau d'une façon différente : $eh$ dans le premier, $f$ dans le second, et $g$ dans le troisième. De cette façon, je me laissais une place vide dans le troisième plateau, ce qui me permettait de maximiser ma dispersion pour le troisième plateau de la première pesée : $i$ à la gauche du fléau, $j$ à droite, et $k$ dans le troisième. Il me restait à placer $l$ : je n'avais de toute façon plus le choix, et le mettait en deuxième position.
Je résumais ce raisonnement relativement complexe par un tableau que je dessinais sur ma dernière feuille de brouillon.
- Première pesée : $abcd \,\,\, \wedge \,\,\, efgh \,\,\, | \,\,\, ijkl $ ;
- Seconde pesée : $aeih \,\,\, \wedge \,\,\, bfjl \,\,\, | \,\,\, cdgk $.
À ce point, il me restait une dernière pesée… et je me décidais à faire un tableau exhaustif, selon l'issue des deux premières pesées. Si j'avais faux, je n'aurais plus de brouillons…
Je notais $\searrow$ une balance qui penchait vers la droite (second plateau plus lourd), $\swarrow$ une balance qui penchait vers la gauche, et $\longleftrightarrow$ une balance dont les poids étaient égaux.
Chaque balance avait trois états, et je faisais 2 pesées : j'aurais donc $3^2 = 9$ combinaisons à tester pour vérifier de façon exhaustive la justesse de mon raisonnement.
Sans plus attendre, je commençais mon tableau…
Possibilités à l'issue des deux premières pesées :
| Résultat des pesées | Conclusion logique |
| $\begin{pmatrix}\swarrow \\ \swarrow\end{pmatrix}$ | (première pesée penche à gauche, seconde pesée penche à gauche) |
| $\begin{pmatrix}\swarrow \\ \longleftrightarrow\end{pmatrix}$ | (première pesée penche à gauche, seconde pesée égale) |
| $\begin{pmatrix}\swarrow \\ \searrow\end{pmatrix}$ | (première pesée penche à gauche, seconde pesée penche à droite) |
| $\begin{pmatrix}\longleftrightarrow \\ \swarrow\end{pmatrix}$ | Possibilités : $\{k^+,j^-,l^-\}$. |
| $\begin{pmatrix}\longleftrightarrow \\\longleftrightarrow\end{pmatrix}$ | Possibilités : $\{k^+,k^-\}$. |
| $\begin{pmatrix}\longleftrightarrow \\ \searrow\end{pmatrix}$ | Possibilités : $\{j^+,l^+,i^-\}$. |
| $\begin{pmatrix}\searrow \\ \swarrow\end{pmatrix}$ | Possibilités : $\{e^+,h^+,b^-\}$. |
| $\begin{pmatrix}\searrow \\ \longleftrightarrow\end{pmatrix}$ | Possibilités : $\{g^+,c^-,d^-\}$. |
| $\begin{pmatrix}\searrow \\ \searrow\end{pmatrix}$ | Possibilités : $\{a^-,f^-\}$. |
Quelque soit l'issue des deux premières pesées, je pouvais déterminer la bille spéciale… et ce qu'elle était.
Je posais mon brouillon à côté de la balance, et entamais mes pesées. Au terme de celles-ci, je pris la bille $l$ en main, la posais dans la borne, et pressais avec assurance le signe $-$.
Le monde commença à trembler. J'eus le temps de me retourner, de voir un petit sourire admiratif sur le visage de $\Delta$, avant d'être aspiré dans un vortex qui convergeait vers mon monde. La dernière image que j'eus du pays mathématique fût ma constante d'intégration, un $\lambda$ comme je l'avais prévu, qui tombait sur le sol de la pièce blanche.
Épilogue
Dans la maison du Supérieur régnait une agitation peu courante. Le videur venait d'entrer par la porte arrière, et préparait avec son hôte le salon à la réception de plusieurs individus.
La première personne à rentrer fut le fils aîné d'un des anciens visiteurs du pays mathématique, suivi de ses deux frères. Le plus âgé s'adressa au Supérieur :
« Il a eu du mal avec la serrure… mais il en est venu à bout. J'en ai profité pour lui donner une leçon qui je l'espère lui sera utile… et je pense qu'il s'en sortira rapidement pour la balance, vu la façon dont il a résolu les énigmes précédentes… »
Il fut coupé dans son élan par un $\Delta$ essouflé, qui venait visiblement de courir toute la distance entre la maison des constantes et la résidence du Supérieur.
« Ça y est, il est parti… je crois que je n'avais jamais vu quelqu'un résoudre ce problème avec une telle rapidité ! ». Il enchaîna, souriant : « alors comme ça, on va pouvoir regoûter un peu à la tranquillité ! Ça faisait un bon bout de temps que ça nous manquait ! »
Le supérieur sourit lui aussi à l'ironie de la remarque, avant de proposer à ses hôtes un whisky coca… ou un coca whisky, au choix.
« Eh bien, oui, nous avons perdu un de nos rares visiteurs… mais je suis sûr qu'au final, nous allons y gagner. Ce bonhomme m'a l'air bien parti pour améliorer notre pays de façon conséquente ! Alors, buvons à sa santé… »
Rapidement, la conversation s'engagea entre les différents protagonistes de cette histoire, chacun y allant de son récit dans un ordre assez décousu… et dont voilà une retranscription exacte, à plusieurs voix.
« En fait, le mec à tes fenêtres continue de marcher ? Quel idiot… »
« Tu lui as encore fait le coup des boîtes ? Tu crois pas qu'un jour, ils vont comprendre qu'elles sont toutes vides ? Il devrait bien le voir, pourtant, que la maison des constantes n'a pas de serrures… »
« Ca me rappelle une bonne blague ! C'est une infinité de mathématiciens qui rentrent dans un bar. Le premier s'avance vers le barman, et… »
« Mais c'est tellement drôle de voir leurs têtes quand ils découvrent la boite vide ! Et puis, je ne tiens pas à prendre… »
« … lui demande un verre de bière. Le second s'approche à son tour… »
« Eh $\Delta$ ! Tu pourrais faire réapparaitre ta lettre par dessus la tête ! On se sent dépaysé sans elle… »
« … le risque qu'ils m'arrachent les boites de la main pour prendre la clé par la force. »
« et commande une moitié de verre… »
« … À mon âge, j'aurais dû mal à les en empêcher ! Et j'aurais l'air bête après… »
« J'aime pas l'afficher ! Ça leur fait peur à leur arrivée s'ils me voient avec un truc qui brille au dessus… »
« … Le troisième s'approche à son tour, et demande un quart de verre… »
« Et tu m'as encore fait passer pour le videur ? »
« Oui mais là, on est entre nous… c'est tellement joli, cette lettre qui brille… »
« Et il te croit ? On devrait bien voir pourtant que j'ai un uniforme de postier ! Le renvoyer dans le grand néant ! Et puis quoi encore ? Lui résoudre l'hypothèse de Riemann pendant qu'on y est ! »
« … Le barman s'énerve, et répond… »
« D'ailleurs, je ne comprends pas que personne n'ait encore trouvé l'astuce… il n'y a pas grand chose à faire pourtant ! »
« Et justement, je ne sais pas si tu as remarqué, mais notre visiteur est né juste cent ans après la mort de Riemann ! Un présage intéressant… »
« On m'a posé un problème intéressant… dans un carré de $n \times n$, combien de carrés de côtés entiers peut on inscrire ? »
« d'une voix tonitruante pour que tous les mathématiciens l'entendent… »
« Trop facile ! Aucun intérêt… »
« Vous n'êtes que des idiots ! Et il leurs remplit deux verres. »
« Cent ans ? C'est vrai que c'est drôle comme coïncidence ! »
« Très bonne, très bonne ! »
« Mais à mon avis, il a trop tendance à réfléchir seul… il risque de s'isoler de la communauté, ca nuira à ses travaux… »
« Bah ! Si ça se trouve, c'est juste de la timidité, mais c'est vrai qu'il est très peu loquace ! »
« Il a l'air d'adorer chercher ! Il sera sûrement extrêmement doué… »
« Et moi, je parie qu'il aura la médaille Fields ! »
« Ça m'étonnerait, il n'a pas le profil idéal… »
Le supérieur interrompit cette joyeuse cacophonie en levant son verre :
« Dans tous les cas, messieurs, je vous propose de porter un toast à notre visiteur… »
Et l'ensemble de l'assemblée reprit avec lui :
« À Grigori Perelman ! »
La suite de la phrase ne fut pas prononcée, mais tout le monde la pensa : « … et aux améliorations qu'il apportera à notre beau pays ! »
Rédaction terminée le 8 décembre 2008.
Mis en forme avec le Typographe
